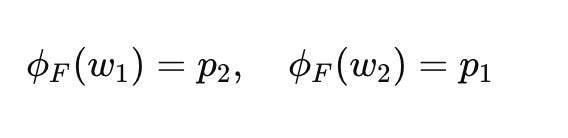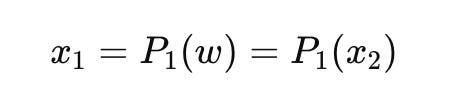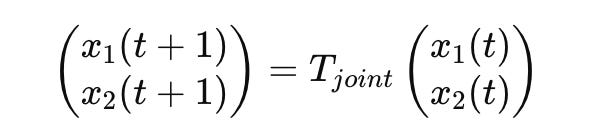Reality Models II: Consciousness and Interface Theory of Perception

Readers will want to be familiar with part I - Reality Models I: Phenomena vs Noumena

This one will be weirder than usual. Much of what will be discussed here is not immediately intuitive and falls both into mathematics and philosophy.

Imagine if the probability our perceptions of the external world depict what is actually there is 0.

We’ve covered the difference between map and territory, phenomena and noumena, inside and outside. Those concepts will be foundational in our approach next to a theory on perception built on evolutionary game theory as proposed by Donald Hoffman.

Hoffman’s metaphor we will attempt to prove and later provide some disproof for is this:

Imagine that all baseline perception is like the desktop of a computer, an interface like a classical black box system, simplified for you, the user. If you drag a folder from your desktop to the trash, does that mean there is a blue folder in the world that you drag to a trashcan? No, they are icons that simplify your interaction with data moving through a circuit board. Imagine then that everything you see, hear, touch, smell, and taste are also icons, symbols that abstract away a much different external world.

What is the circuit board to your perceptions?

This is a very Kantian question and conjures “map is not the territory” and the phenomena/noumena dichotomy.

But Hoffman doesn’t merely propose the thought experiment itself. He approaches it rigorously.

Note on intent.

Why keep this multiple part series going? I published the first part of “Reality Models” on March 21, 2023. That was a very different time - as much as for myself as for you the reader. Life moves often like punctuated equilibrium. You will have long stretches of very little and then sudden explosions of insight or change. Phil Hine, the occultist and author describes the ascent to gnosis as like “a snake sloughing off its skin… so too, we must be prepared to slough off old patterns of thought, belief and behavior that are no longer appropriate for the new phase of our development.” Here this is the same. Starting in autumn 2023 I paused producing theory, scientific, or mystical writing to instead pursue gnostic experience, to focus on fiction, and to descend quite literally into the underworld. Orpheus enters Hades once in pursuit of of Eurydice. He descends once and exits never to return to Hades again while alive because the living can’t pass through Hades twice. So here we are back in the land of the living, with conversations and insights from Tartarus, and plenty of research to go with it. Thanks to my readers for holding on since the first part of this series. Going forward this will be more freeform moving through philosophy, mathematics, and the occult to build a theory of what is, and is not.

Introduction

Hoffman’s hypothesis suggests that our perceptions do not accurately represent reality. Instead they function as an adaptive interface that aids in survival, akin to a user interface on a computer - which hides the complex operations of the machine and presents only what the user needs to know to operate effectively.

The theory posits that what we perceive is not necessarily what is true but instead what is useful for our survival. Interface theory of perception hinges on what Hoffman calls fitness tradeoffs

1. Fitness vs. Truth:

   1. In the evolutionary game, organisms that perceive objective reality maybe less fit compared to those whose perceptions are distorted but more useful for survival. The idea is that seeing “truth” might be less advantageous than seeing what is merely fitness-enhancing. For example, an organism that perceives nutritious food more effectively than it perceives accurate details about the environment might have a better chance at survival

2. Simplified Perceptions

   1. Hoffman proposes that our perceptions simplify the complexity of the world, focusing on information that directly impacts survival and reproduction. That means that much of what we perceive is not a true reflection of objective or noumenological reality but is rather a useful fiction that aids in making survival decisions.

What is inner experience?

We assume perceptions describe an accurate representation of something. What that something is - is assumed to be objects in space external to our perception of them. It takes a leap to be more critical about what perceptions actually are. Recall the apple thought experiment in Reality Models I: Phenomena vs Noumena, is there really an apple? We can’t know insofar as all cognition of perception is an internal map of an external territory. How faithful the map’s representation of the external territory depends on who you ask, and depends on which models you are using.

First we need to establish which assumptions we are questioning so let’s establish two basic ones:

1. Natural selection favors true perceptions

2. The mind is what the brain does

Hoffman would ask, “why these assumptions?”

For one, they are rigorously testable.

They are central to a standard model of perception. If you are to take space time, quantum mechanics, even the fundamental laws of thermodynamics as givens, you need to establish that perceptions are accurate, that our process of natural selection favors true perceptions by default, and that mind arises from the processes of the brain. Establishing a cause and effect chain here is required for the standard models of science to work. Something like:

brain activity → stimulus perceived in mind

or even:

external physical event → visual input → brain activity → stimulus perceived in mind

What we then have is a problem of cause and effect chains. Which cause actually leads to which effect? And furthermore, what is the most irreducible state we can get down to? The common assumption here is space time.

Among conflicting hard question of consciousness theories, whether they are monism, dualism, neuronal microtubules, casual architectures, neuronal workspaces, or even user illusions/attentional schemas, they all rely on space time as a fundamental assumption.¹

Next we will break down what perceptual strategies are in natural selection, and why they do not require space time as a foundational assumption.

Perceptual Strategies

Before diving into the technicals below, what are we asking here?

If an organism is to survive it needs to balance caloric burn with its metabolism. An organism that consumes too many calories to some goal, will not pass what Hoffman calls fitness tests. Similarly, an organism that burns too few calories to achieve some goal will also not pass a fitness test. Here if the goal is perception, and a faithful representation of the outside world then it follows that : any organism must burn enough calories to faithfully represent the external world to pass fitness tests (survival and procreation), but not so many calories as to represent the external world as an inner experience too faithfully, as to burn too many calories at the expense of fitness.

What does evolution tell us about perception? What kinds of perception does evolution favor? What kinds of perceptual models are more likely to go extinct? Above we established a first assumption, “natural selection favors true perceptions”. First we will need to establish definitions. What is a kind of perception?

For a basic model of perceptual strategies, Hoffman defines the objective world by some set W and the perceptions of an organism by some set X where we assume no knowledge of X or W. Next the perceptual strategy is defined as a function P, from W to X. That is ( P: W→X )

Hoffman explains:

²

Hoffman distinguishes classes of perceptual strategies by what our assumptions are about each variable and the function above. He breaks these into classes in order of strongest to weakest assumptions:

1. naive realism - Perceptions are identical to the world. That is : (x = w) where P is the identity function.

2. strong critical realism - Perceptions are identical to a subset of the world. That is : (X⊂W) where P is the identity function of the subset.

3. weak critical realism - Perceptions need not be identical to any subset of the world, but, the relationships among our perceptions accurately reflect relationships in the world. That is : it is allowed that (X ⊂/ W) but required that P is a homomorphism of structures on W, where a homomorphism is a structure preserving map of two algebraic structures of the same type. In this case a linear vector map.

4. interface perceptions - Perceptions need not be identical to any subset of the world, and relationships among perceptions need not reflect relationships in the world except measurable relationships (probability relationships only). That is : It is allowed that (X ⊂/ W) and that P is not a homomorphism of the structures on W, except for measurable structures.

5. arbitrary perceptions - Perceptions need not be identical to any subset of the world, and that the relationships among our perceptions need not reflect any relationships in the world. That is : it is allowed that (X ⊂/ W) and P is not a homomorphism of any structure on W.

Hoffman shows the relationships between five classes of perceptual strategies below:

³

Even among strict physicalist theories on perception, few researchers embrace naive realism. Every class of organism perceives “reality” differently. Given an external W, you will find a wife variety of states X across organisms, sensory organs, and cognitive maps. Some animals see more color variants and light spectrums than we do, some see fewer, others see none. There is no known “total model” for the external W, as each internal X, relies on circumstances of evolution, and the fitness tradeoffs related to each species.

Evolutionary Game Theory: Fitness beats truth, every time.

First off let’s break down how the math here works.

1. Utility Functions:

   1. In these models, different perceptual strategies are associated with different utility functions that measure ‘fitness’ of an organisms given its perceptions. These functions do not map directly to truth but rather to the organism’s survival and reproductive success.

2. Evolutionary Dynamics:

   1. Using equations from evolutionary dynamics, Hoffman shows that over time, strategies that maximize fitness (even at the expense of truth) become more prevalent in the population.

3. Monte Carlo Simulations:

   1. Hoffman and his team use Monte Carlo simulations to explore behavior of populations over many generations. These simulations repeatedly play out the evolutionary game under different conditions to see which strategies dominate.

We’ll revisit this math in the next section for a comprehensive fitness beats truth theorem

Interface Theory of Perception’s most radical proposal is formalized and tested evolutionary games.

Next let’s define evolutionary game theory.

Game theory itself is the study of mathematical models of strategic interactions between players or agents. It was pioneered by John Von Neumann with mixed-strategy two person zero sum games where one player’s gains equal the second player’s net loss. Game theory models different types of competitive and cooperative games between two or larger groups of players and are useful in modeling economics, systems science, logic, international relations, biology, etc. Most notable is John Nash’s work at the RAND Corporation applying Nash equilibrium to corporate and global policy decisions. Here we will focus on games as they apply to population evolution which differs from classical game theory as it focuses on strategy change.⁴

For evolutionary game theory we need to establish:

• Who is making decisions - agency

• With whom does interaction occur - assortativity

• Behavior and dynamics

Agency

On agency we can break down levels of agency for a single agent (organism) in game. A good example is set of individuals N, such that individual i ∈ N adopts some strategy si ∈ Si. Let S be the set of strategy profiles, such that S =Xi∈N Si. When strategy updating occurs, instead of an individual i ∈ N following an individualistic strategy updating rule of the form.

You can use a coalitional T ⊆ N to update ST ∈ ST by updating to

For coalitional better response dynamic this can be generalized so that T ⊆ N chooses a strategy sub-profile that weakly benefits all of its members. That is, coalition T chooses a coalitional better response from the set

Here we are dealing with multiple agency variants of best and better response dynamics. Let’s use the example of “Changing Partners” from Patti Page. At some weddings, after the marrying couple has started dancing, other couples join the dancing. Some couples join the dancing early, while others wait until a large proportion of people are dancing, so we have something like collective versions of threshold models.

We can also have coordination games on networks demonstrating collective agency, matching coalitions, and social choice rules.

Assortativity

Here we are exploring preferences with regards to prisoner’s dilemmas

Evolution according to Hoffman, is reducible to a mathematically precise theory. In evolutionary game theory there is a notion of fitness payoffs. Fitness payoffs depend on whatever the state of the world is, but also depend on the state of the organism, say, hungry, full, feeding, fighting, fleeing, mating, etc. If a lion is hungry, a gazelle gives a fitness payoff. If a lion is full and needs to mate, another lion gives a fitness payoff. If reversed there is no payoff. Therefore you have, organism type, organism state, and external world. For a gazelle, having meat gives no fitness payoff value.

Fitness payoffs are a function given a range :

(state of world + structure) → finite state of payoff values (0-100), where 0 is low payoff and 100 is maximum payoff.

Organisms learn to behave in ways that maximize fitness payoffs given state and external environment.

If evolution tunes us to maximize fitness payoffs, then the technical question that follows is this: are the fitness payoffs, functions that preserve the structure of the world? Are fitness payoffs homomorphisms of structures in the objective external, phenomenological world? What is the probability that a randomly chosen payoff function will be a homomorphism of an external structure given n states in the world given m payoff functions. What fraction of payoff functions are homomorphisms? Where n and m approach infinity?

This is where things get strange. What if it is 0? What if no fitness payoffs demand a homomorphism? What if fitness payoffs don’t need perceptions to be accurate at all?

Hoffman uses these examples:

Consider a game in which two animals compete for a resources. The quantities of resources might vary within a range set. With repeating games we can apply different resource quantities to payoff functions. If we’re dealing with a finite resource like water, you can have high yields, mid yields and low yields that correspond to higher fitness payoffs down to lower fitness payoffs. Hoffman explains :

---

Once we have the distribution of resources and the fitness payoff function, we can then compute the expected payoffs that different perceptual strategies would obtain when competing with each other. For instance, if some animals use an interface strategy (IS) and others a weak critical realist strategy (WS), we can compute the expected payoff to an IS animal when it competes with a WS, the expected payoff to an IS animal when it competes with another IS, the expected payoff to a WS when competing with an IS, and the expected payoff to a WS when competing with another WS. There are 2 x 2 = 4 such expected payoffs to compute. If there is a third strategy, say some animals use a strong critical realist strategy (SR), then we can compute the 3 x 3 = 9 different expected payoffs; if there is a fourth strategy, then there are 16 such payoffs, and so on. Given these expected payoffs, there are formal models of evolution that we can use to predict which strategies will dominate, coexist, or go extinct. 37−40 We can, for instance, use evolutionary game theory, which assumes infinite populations of competing strategies with complete mixing, in which the fitness of a strategy varies with its relative frequency in the population. In the case in which just two strategies, say S1 and S2 , are competing, we can write down the four expected payoffs in a simple table, as shown in Figure 4. The expected payoff to S1 is a when competing with S1 and b when competing with S2 ; the expected payoff to S2 is c when competing with S1 and d when competing with S2 .

Then it can be shown that S1 dominates (i.e., drives S2 to extinction)

if a>c and b>d; S2 dominates if a<c and b<d; they are b is stable

if a>c and b<d; they coexist if a<c and b>d; they are neutral if a = c and b = d . Similar results can be obtained when more

strategies compete, but new outcomes are possible. For instance, with three strategies, it might be that S1 dominates S2 , S2 dominates S3 and S3 dominates S1 , as in the popular children’s game of Rock-Paper-Scissors in which rock beats scissors, which beats paper, which beats rock. With four or more strategies, the dynamics can have more complex behaviors known as limit cycles and chaotic attractors.⁵

---

When enough of these game trials are run, with realist and interface perceptual strategies run against each other on a scale from naive realism to interface perceptions, in most cases realist strategies are driven to extinction.

Imagine a fitness payoff function in which resources vary from 1 to 100, where payoff is greatest for intermediate quantities of the resource. 5(B) illustrates a realist perceptual strategy that can only see two colors red and green, which is realist because it the colors bind to resource quantity. All green spaces have higher resources than red. 5(C) by contrast does not accurately bind color to perception, but instead uses interface in a not realist strategy to accurately assess the higher payoff for intermediate quantity, at the expense of an objective representation of reality.

Ultimately what evolutionary game theory presents is this: fitness and truth are distinct. Perceptual strategies tuned to fitness will outcompete those tuned to truth. Truer perceptions are not fitter perceptions.

This is extremely important: evolution does not “care” about truth when it comes to perception, evolution only “cares” about fitness. “the principle chore of brains is to get the body parts where they should be in order that the organism may survive”, says Patricia Churchland. The difference here is between informal accounts of evolution and a treatment by measurement.

Now let’s run the actual math

Fitness Beats Truth Theorem

1. Perceptual Strategies and Utility Functions

Hoffman posits that organisms have perceptual strategies, which are functions 𝜙 mapping states of the world 𝑊 to perceptions P:

ϕ:W→P

However instead of focusing on accuracy, these strategies are judged by how they enhance fitness. Fitness is typically represented by a utility function U that assigns a fitness value to each perception.

U(ϕ(w))

where 𝑤 ∈ 𝑊 is a state in the world, and 𝜙(𝑤) is the perception of that state. The utility function 𝑈 reflects how well the perception 𝜙(𝑤) helps the organism to survive and reproduce.

2. Fitness vs. Truth

To model the relationship between fitness and truth, Hoffman considers two types of perceptual strategies:

• Truth-Tracking Strategy

  • ϕT: Maps states of the world to accurate perceptions. If the world is 𝑤, then the perception is 𝜙𝑇(𝑤), which is an accurate representation of 𝑤.

• Fitness-Maximizing Strategy

  • ϕF: Maps states of the world to perceptions that maximize fitness, even if they are not accurate.

The goal is to compare the fitness 𝑈(𝜙𝐹(𝑤)) with 𝑈(𝜙𝑇(𝑤))

3. Evolutionary Dynamics

To analyst the evolution of these strategies, Hoffman uses the following from evolutionary game theory. The fitness of an organism using a particular strategy ϕ is given by:

where 𝑝(𝑤) is the probability distribution over the states of the world 𝑊

4. Fitness-Beats-Truth Theorem (FBT Theorem)

The FBT Theorem states that under certain conditions, a fitness-maximizing strategy 𝜙𝐹 will outperform a truth-tracking strategy 𝜙𝑇 in terms of evolutionary success. This is formalized by showing that:

for a range of environments W

Heres an example:

Consider a simple world with two states 𝑊={𝑤1,𝑤2} and two perceptions 𝑃={𝑝1,𝑝2}. The truth-tracking strategy might be:

and the fitness-maximizing strategy could be:

Suppose the utility functions are:

Clearly, 𝑓(𝜙𝐹)>𝑓(𝜙𝑇), showing that the fitness-maximizing strategy 𝜙𝐹 provides a higher overall fitness than the truth-tracking strategy 𝜙𝑇

5. Monte Carlo Simulations

Hoffman often uses Monte Carlo simulations to explore the evolutionary dynamics of these strategies. The simulations involve running many iterations where organisms with different strategies compete, reproduce, and die off. These simulations typically reveal that strategies maximizing fitness, even at the expense of truth, become dominant over time.

The key takeaway from Hoffman's mathematical approach is that in evolutionary scenarios, the strategy that enhances fitness (even if it distorts reality) tends to outperform a strategy that tracks truth. The math here is centered around utility functions and evolutionary dynamics, illustrates how perceptions shaped by fitness considerations can dominate even when they do not accurately reflect the underlying reality.

Once you get through the formulas, the proposition Hoffman is making here is extremely weird and challenges the traditional view that our perceptions must be accurate to be advantageous.

Cause and effect chain: Minds and brains - an overview of conscious agents.

John Locke questions in Essay Concerning Human Understanding 1690, whether it is possible that the colors perceived by one man’s eyes are faithfully represented by another man’s eyes. Obviously there is overlap but internal maps are what make you, you.

A conscious agent is a mathematical model of consciousness that Hoffman suggests could underlie all experiences and perceptions. In his framework, a conscious agent is defined by its ability to experience, decide, and act. The interactions of these agents give rise to what we perceive as the physical world.

Think about Gottfried Wilhelm Leibniz’s “Monadology” or the Buddhist/Hindu Jewel Net of Indra, they are each conceptually similar models.

A conscious agent can be described by a triple 𝐴=(𝑋,𝐺,𝐷), where:

• 𝑋: A set of possible conscious experiences.

• 𝐺: A set of possible actions the agent can take.

• 𝐷 A decision function that determines the agent's actions based on its experiences.

Hoffman’s mathematical model of conscious agents involves several components, including state spaces, perception functions, and action functions. The key idea is that conscious agents interact with each other through these functions, and these interactions produce the phenomena we can observe.

1. State Space and Perception:

Let 𝑋 represent the state space of all possible conscious experiences an agent can have. A conscious agent's state at any given time is a point 𝑥 ∈ 𝑋

• Perception Function 𝑃: Maps the state space of the world 𝑊 (which could be the states of other agents) to the state space of experiences 𝑋. The perception function captures how an agent perceives the world.

• World State w: A point in the world space 𝑊. The perception of this world state by an agent is given by 𝑥=𝑃(𝑤).

2. Action Space and Action Function :

Let 𝐺 represent the set of possible actions an agent can take.

• Action Function 𝐴: Determines the action 𝑔∈𝐺 that an agent will take based on its current experience 𝑥∈𝑋.

The action 𝑔=𝐴(𝑥) influences the world and, consequently, affects the experiences of other agents.

3. Markovian Dynamics of Conscious Agents:

Hoffman often models the dynamics of conscious agents using Markov chains. The idea is that the state of a conscious agent evolves over time according to a Markov process, where the future state depends only on the current state.

• State Transition: The transition from one state to another in the space of experiences 𝑋 can be represented by a transition matrix 𝑇, where:

• Update Rules: The agent’s state at time 𝑡+1 is determined by its state at time 𝑡, the perception function, and the transition matrix:

Ok now for the example of a network model of conscious agents:

Have you ever been in a K-Hole? This is very similar

Interacting Conscious agents:

Consider two conscious agents, 𝐴1 and 𝐴2, with state spaces 𝑋1 and 𝑋2, action spaces 𝐺1 and 𝐺2, and decision functions 𝐷1 and 𝐷2.

• Perception: Each Agent percieves the other’s state. For agent A1, the perception might be:

where x2 is the state of A2, and vice versa for A2

• Action: Each agent takes actions based on its perception. For A1:

The action g1 affects the state of A2, thus changing x2, which in turn changes x1, and the cycle continues.

• Interaction Dynamics: The interactions between these agents can be represented by coupled Markov chains. The state of the system evolves according to the joint transition matrix 𝑇𝑗𝑜𝑖𝑛𝑡, which accounts for the interactions between 𝐴1 and 𝐴2 :

This formalism can be extended to any number of interacting conscious agents, leading to a complex network of interactions. The global behavior of this network can give rise to emergent phenomena, such as the shared experiences of a physical world. This provides a rough, but kind of interesting model for Leibniz’s network consciousness in the “Monadology”

5. Compositionality of Conscious Agents:

Another important aspect is the compositionality of conscious agents. Hoffman proposes that simple conscious agents can combine to form more complex agents. This compositionality is analogous to how simpler systems in physics combine to form more complex systems.

• Compositional Structure: If 𝐴1 and 𝐴2 are two conscious agents, they can combine to form a new agent 𝐴3=𝐴1⊕𝐴2, with its own state space 𝑋3, which is a product of the state spaces of 𝐴1 and 𝐴2:

Then the dynamics of A3 are governed by the joint dynamics of A1 and A2.

So what exactly are we talking about here? The implications are, again… weird.

Hoffman is modeling the fundamental process underlying consciousness and perception. His model treats consciousness as a fundamental aspect of reality, and interactions between conscious agents reverse the cause and effect chain mentioned earlier. Let’s reverse it

Instead of:

external physical event → visual input → brain activity → stimulus perceived in mind

We have:

stimulus perceived in mind → brain activity → visual input → external physical event

Spooky right? the implications here and very cool

They give rise to the phenomena we observe in the physical world. Here with state spaces perception/action functions, decision-making processes, and the dynamics of agent interaction - with with Markov chains and compositionality, Hoffman’s theory proposes a way to understand how complex consciousness and the physical world emerge from the interactions of conscious agents.

You are a conscious agent, I am a conscious agent. Those are the only things that actually exist according to Hoffman. The space between, space time, objects, events, time, all of it is abstraction. Space time, narrative, events, symbols, they are the abstraction of an interface that bridges between conscious agents. The computer or phone you are reading this on, according to Hoffman doesn’t exist. Only you, the other agents and I do. all the stuff in between is merely abstraction, it’s the black box, the interface.

What does this all mean?

I highly recommend watching the following two Hoffman’s interviews below. They clarify a lot of this. Interface theory does not necessarily validate some of the tenets of Pansychism, but it opens some interesting doors, and provides a curious model for Kant’s “Critique of Pure Reason” founded in empiricism.

This piece took a while and came out of a protracted period of study and isolation. Next time we’ll explore some counter arguments against Hoffman’s game theory results, and after move into stranger places via the more mystic doors these ideas open.

1. Hoffman, Prakash, Prentner “Fusions of Consciousness” Entropy 2023 25(1), 129

2. Hoffman “Consciousness and the Interface theory of Perception” p 5.

3. Hoffman “Consciousness and the Interface theory of Perception” p 6.

4. Newton, Johnathan, “Evolutionary Game Theory, A Renaissance”, Games ISSN 2073-4336 MDPI Basel Vol 9 ISS 2 pp 1-67

5. Hoffman “Consciousness and the Interface theory of Perception” p 9